Derivatives tell us the rate of change of the derived function. If f'(x_0) > 0 then f at x_0 is increasing, if f'(x_0) < 0 it is decreasing. Refer to functions for more information.
For f(t) first and second derivative:
| function | derivative with respect to x |
|---|---|
| Ax^B | ABx^{B-1} |
| f(x)g(x) | f'(x)g(x) + f(x)g'(x) |
| \frac{f(x)}{g(x)} | \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)} |
| \sin{x} | \cos{x} |
| \cos{x} | -\sin{x} |
| \tan{x} | \frac{1}{\cos^2{x}} |
| \cot{x} | -\frac{1}{\sin^2{x}} |
| \arcsin{x} | \frac{1}{\sqrt{1-x^2}} |
| \arccos{x} | -\frac{1}{\sqrt{1-x^2}} |
| \arctan{x} | \frac{1}{x^2+1} |
| arccot\ x | -\frac{1}{x^2+1} |
| f(g(x)) | f'(g(x))g'(x) |
| e^x | e^x |
| \ln(x) | \frac{1}{x} |
| a^x | \ln(a)a^x |
| \log_a(x) | \frac{1}{x\ln(a)} |
To find a tangent line to a function at a given point we can use the following formula: y = f(x_0) + f'(x_0)(x - x_0) where (x_0, f(x_0)) is the point where we are trying to find the tangent line.

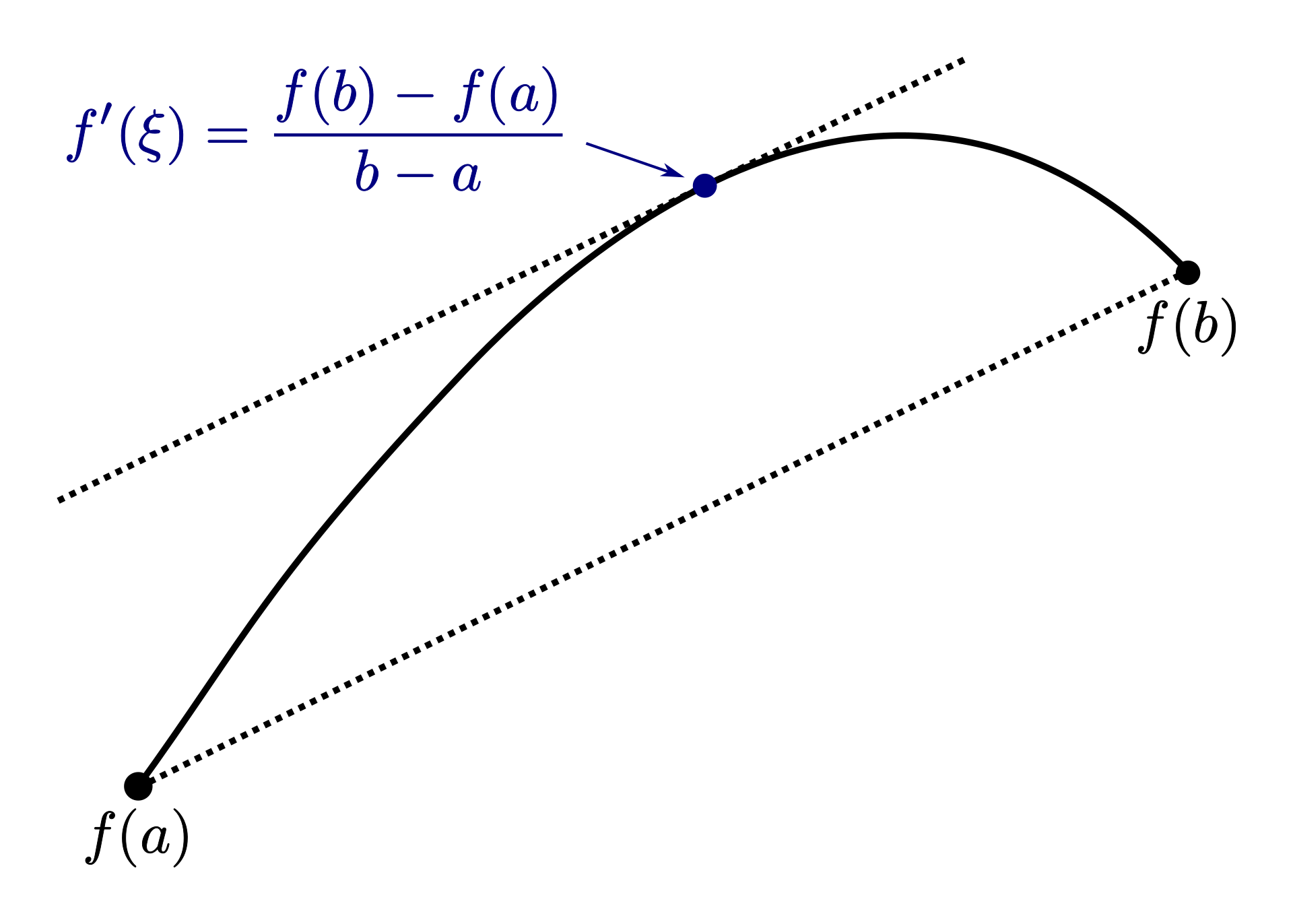
If a function is continuous at [a;b] and differentiable at (a;b) then (\exists x_0)(f'(x_0) = \frac{f(b) - f(a)}{b - a})