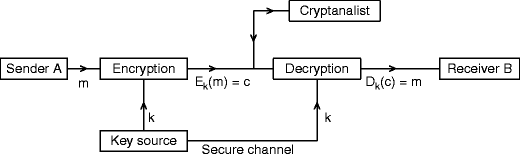
Used for privacy of communication (confidentiality).
vs security
vs coding theory
vs cryptanalysis
For a message X
Key is the same for the sender and receiver. The keys have to be confidentially shared. A message authentication code is used to ensure authentication and integrity.
Problem: we must establish a symmetric key. Key agreement protocol.
Public key is shared with A + I from receiver to sender. Only receiver can decrypt.
Problem: we must authenticate the public key.
Offset the alphabet by some amount
Rather than offsetting the alphabet by a fixed amount, permute the whole alphabet. This gives |\Sigma|! permutations. This is still susceptible to statistical attacks (for example in english some letters are more common than others).
Establish a key. Slide it over the text to encode and “add” letters. This is essentially addition modulo |\Sigma|. Group \mathbb Z_{|\Sigma|}. Now both the key length and key content has to be found to decipher.
Example: \text{f} + \text{c} = \text{h} or \text{x} + \text{d} = \text{a}
Explore repeated n-grams and check likeliness of them occurring.
Say in a string (x_1x_2 \cdots x_{313}) of 313 characters where |\Sigma| = 26 the same trigram appears 5 times. The string has n = 311 trigrams. Let t_i = x_ix_{i+1}x_{i+2}. The number of occurrences of some trigram n_{abc} = \sum_{i = 1}^n 1_{t_i = abc}.
Let t_i be independent and uniformly distributed. There are \frac{1}{p} = 26^3 = 17576 possibilities. P[n_{abc} = t] = \binom{n}{t} p^t (1 - p)^{n-t}. By approximation with Poisson distribution we get P[n_{abc} \ge 5] \approx 2.42 \cdot 10^{-7}. Which is very unlikely for a random string. This can be used to conclude that the string isn’t exactly random.
The position of appearance of repeating n-grams can tell us about the length of the key. The gcd of positions is a good indicator.
\begin{aligned} \text{Index}(x_1, \cdots, x_n) &= P_{I, J}[x_I = x_J | I \ne J] \\ &= \frac{1}{n(n - 1)} \sum_{1 \le i, j \le n, i \ne j} 1_{x_i = x_j} \\ &= \sum_{c \in Z} \frac{n_c(n_c - 1)}{n(n - 1)} \\ \end{aligned}
where I, J \in \{1, \cdots, n\} are independent and uniformly distributed.
The index of coincidence is invariant over substitution and transposition
\text{Index}(x_1, \cdots, x_n) = \text{Index}(\sigma(x_1), \cdots, \sigma(x_n)) = \text{Index}(x_{\rho(1)}, \cdots, x_{\rho(n)})
For some permutation \sigma over Z and permutation \rho of \{1, \cdots, n\}
\begin{aligned} E(\text{Index}(x_1, \cdots, x_n)) &= \frac{1}{n(n - 1)} \sum_{1 \le i, j \le n, i \ne j} P[x_i = x_j] &= \sum_{c \in Z} f_c^2 \end{aligned}
if all x_i have iid distribution with frequency table f_c. For a random string over a 26 letter alphabet the value tends to 0.038, while for english it tends to 0.065. This fact can be used to detect the correctness of our chosen key length.
Electro-mechanical encryption device. The description of the machine was public. First computers where constructed to break the enigma machine.
Given a permutation \sigma over Z = \{A, B, \cdots, Z\}
The secret key consists of:
The encryption of a character is then as follows:
y_i = \sigma^{-1} \circ \alpha^{-1}_{i_1} \circ \beta^{-1}_{i_2} \circ \gamma^{-1}_{i_3} \circ \pi \circ \gamma_{i_3} \circ \beta_{i_2} \circ \alpha_{i_1} \circ \sigma(x_i)
where i_3i_2i_1 are the last three digits of the basis 26 numeration of i + a.
The entropy of enigma is 57 bits.
For any distribution of X over an abelian group G, Y is independent from X and is uniformly distributed.
Number of bits of information to represent a value X is H(X)
H(X) = -\sum_{x \in X} P[X = x]\log_2P[X = x]
H(X, Y) = -\sum_{x \in X}\sum_{y \in Y} P[X = x, Y = y]\log_2P[X = x, Y = y]
H(X | Y) = -\sum_{x \in X}\sum_{y \in Y} P[X = x, Y = y]\log_2P[X = x | Y = y]

\forall_{x, y} P[Y = y] \ne 0 \implies P[X = x | Y = y] = P[X = x]
Can be also stated as saying that X and Y are independent. Or can be stated as H(X|Y) = H(X).
So the adversary learns nothing about X by intercepting Y. Vernam cipher provides perfect secrecy.
Perfect secrecy implies H(K) \ge H(X). This means to achieve perfect secrecy the number of possible keys has to be as large as the number of possible messages. This means we cannot do anything better than the Vernam cipher. This also means that X have a finite support.