1 RSA

1.1 Euler totient function

\varphi(n) is the number of coprimes to n.

1. |Z^*_n| = \varphi(n)
2. for all x \in Z_n we have x \in Z_n^* \iff gcd(x, n) = 1
3. Z_n is a field \iff Z_n \setminus \{0\} \iff \varphi(n) = n - 1 \iff n is prime
4. for all x \in Z_n^* we have x^{\varphi(n)} \equiv 1 \pmod n
5. if e such that gcd(e, \varphi(n)) = 1 we let d = e^{-1} \bmod \varphi(n). For all y \in Z_n^*, y^d \bmod n is the only e’th root of y modulo n

• \varphi(p) = p - 1 when p is prime
• \varphi(mn) = \varphi(m)\varphi(n) when m and n are coprime
• \varphi(p^a) = (p - 1)p^{a-1} when p is prime
• \varphi(p_1^{a_1}, \cdots, p_r^{a_r}) = (p_1 - 1)p_1^{a_1-1} \cdot \ldots \cdot (p_r - 1)p_r^{a_r-1}

1.2 chinese remainder theorem (CRT)

Let m and n be two integers such that gcd(m, n) = 1. For any a, b \in \Z there exists x \in \Z such that

x \equiv a \pmod m

x \equiv b \pmod n

For all such solutions, x \bmod (mn) is unique.

f: Z_{mn} \to Z_m \times Z_n is a group isomorphism f(x) = (x \bmod m, x \bmod n). Then f^{-1}(a, b) = an(n^{-1} \bmod m) + bm(m^{-1} \bmod n) \pmod{mn}

1.2.1 equality modulo composite numbers

For any a, b, m, n \in \Z such that gcd(m, n) = 1 then

\begin{cases} a \equiv b \pmod m \\ a \equiv b \pmod n \\ \end{cases} \iff a \equiv b \pmod{mn}

1.2.2 CRT backwards

Let m, n be two integers such that gcd(m, n) = 1. Let u = n(n^{-1} \bmod m) and v = m(m^{-1} \bmod n) then g: (a, b) \mapsto au + bv \bmod{mn} is a ring isomorphism.

1.3 trial division

Given an integer we output a list of primes whose product is equal to n.

i = 2
x = n
for _ in 2:sqrt(n)
    while i divides x
        output i
        x = x / i
    i = i + 1

if x > 1
    output x

1.4 fermat test

Utilizing the little fermat theorem. Might call something a prime that isn’t a prime.

for _ in 1:k
    b = random(1, n)
    x = b^(n-1) mod n
    if x != 1
        return "not prime"

return "maybe prime"

1.5 carmichael numbers

n is a carmichael number iff it is composite and \forall_{\{a : gcd(a, n) = 1\}} a^{n-1} \equiv 1 \pmod n

1.6 miller-rabin test

We can write n - 1 as 2^st for t odd. When n is prime then b^{n-1} \bmod n = ((b^t)^2\cdots)^2 \bmod n = 1

if n = 2
    return "prime"

if n is even
    return "composite"

n === 2^s * t + 1

for _ in 1:k
    b = random(1, n)
    x = b^t mod n
    i = 0
    if x != 1
        while x != n - 1
            x = x^2 mod n
            i = i + 1
            if i == s or x == 1
                return "composite"

return "maybe prime"

Complexity: O(k\ell^3)

An integer is prime iff it passes the miller-rabin test for all b \in Z_n^*. If more than a quarter of b \in Z_n^* pass the miller-rabin then all b \in Z_n^* do.

So P[\text{output maybe prime}|\text{n composite}] \le 4^{-k}.

1.7 prime number generation

Let p(N) denote the number of prime numbers up till N. Then p(N) \sim \frac{N}{\ln N}. So the chance of a \ell bit number to be prime is \frac{1}{\ell \ln 2}. We then apply miller-rabin test to check if the number is prime. If not, try again. Complexity: O(\ell^4).

If we let k = \frac{1}{2}(\log_2\ell - \log_2\varepsilon) then P[\text{output is not prime}] \le O(\ell) \cdot 4^{-k} = O(\varepsilon)

1.8 RSA cryptosystem

• Public parameter: \ell
• find two random different prime numbers p and q of size \frac{\ell}{2} bits. Set N = pq. Select e such that gcd(e, (p - 1)(q - 1)) = 1
  • pick e random until it is valid
  • popular choice are e = 17 and e = 2^{16} + 1. They are prime (so likely to be coprime with (p-1)(q-1)) and have a simple bit representation for raising power when encrypting
• an element x \in Z_N
• pk = (e, N)
• sk = (d, N) where d = e^{-1} \bmod \varphi(N)
• y = x^e \bmod N
• x = y^d \bmod N

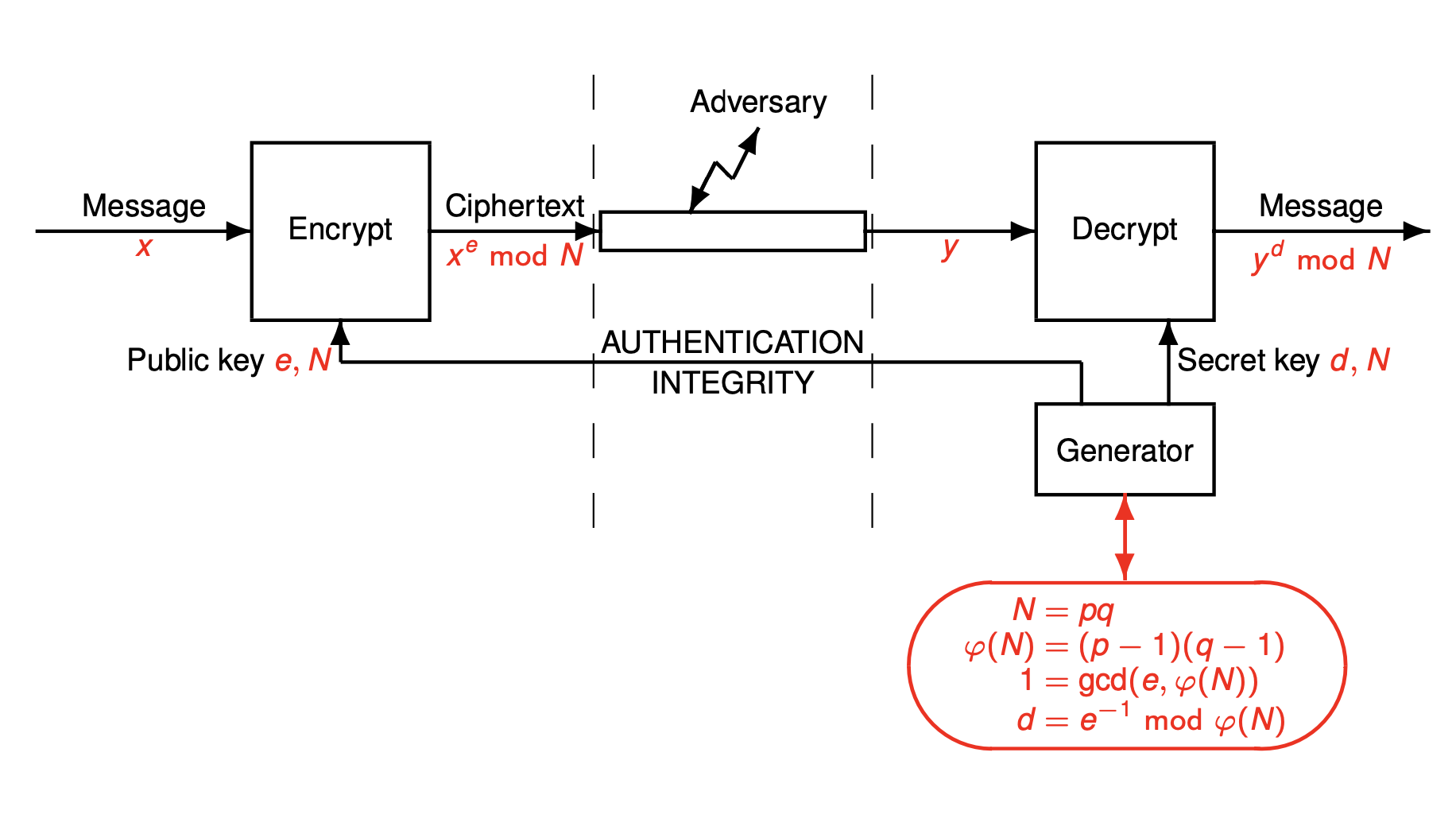
For any x \in \{0, \cdots, N-1\} and any k we have x^{k \varphi(N)+1} \bmod N = x

1.8.1 complexities

RSA with modulus of \ell bits:

• Generation: O(\ell^4)
• Encryption: O(\ell^3) (or O(\ell^2) if e is constant)
• Decryption: O(\ell^3)

1.9 quadratic residuosity

1.9.1 square roots in finite fields

Let K be a finite field. For any x \in K we have x^2 = 1 \implies x = 1 \lor x = -1.

1.9.2 existence

Let p be an odd prime number. Then b \in Z_p^* has a square root if and only if b^{\frac{p-1}{2}} \bmod p = 1. Then b is called a quadratic residue.

1.9.3 Z_p when p \equiv 3 \pmod 4

Let p be a prime number such that p \equiv 3 \pmod 4. For any x \in Z_p we have y^2 \equiv x \pmod p \implies y \equiv x^{\frac{p+1}{4}} \pmod p \lor y \equiv -x^{\frac{p+1}{4}} \pmod p.

1.9.4 Z_n when n = pq

let p and q be two different prime numbers and n = pq. Let x \in Z_n and a and b such that

\begin{aligned} x \equiv a^2 \pmod p \\ x \equiv b^2 \pmod q \\ \end{aligned}

We have

x \equiv y^2 \pmod n \iff \begin{cases} y \equiv \pm a \pmod p \\ y \equiv \pm b \pmod q \\ \end{cases}

1.9.5 legendre symbol

For p an odd prime

\left(\frac{b}{p}\right) = \begin{cases} 0 & \text{if } b \bmod p = 0 \\ 1 & \text{if b is a quadratic residue in } Z_p^* \\ -1 & \text{if b is not a quadratic residue in } Z_p^* \\ \end{cases}

1.9.6 jacobi symbol

For n odd

\left(\frac{b}{n}\right) = \left(\frac{b}{p_1}\right)^{\alpha_1} \cdot \ldots \cdot \left(\frac{b}{p_r}\right)^{\alpha_r}

For the factorization of n.

So b \in Z_p^* is a quadratic residue \iff \left(\frac{b}{p}\right) = 1. So b \in Z_n^* is a quadratic residue \implies \left(\frac{b}{n}\right) = 1.

Properties:

• \left(\frac{1}{b}\right) = 1 for b odd
• \left(\frac{a}{b}\right) = \left(\frac{a \bmod b}{b}\right) for b odd
• \left(\frac{ab}{c}\right) = \left(\frac{a}{c}\right)\left(\frac{b}{c}\right) for c odd
• \left(\frac{2}{a}\right) = 1 if a \equiv \pm 1 \pmod 8 and \left(\frac{2}{a}\right) = -1 if a \equiv \pm 3 \pmod 8 for a odd
• \left(\frac{a}{b}\right) = -\left(\frac{b}{a}\right) if a \equiv b \equiv 3 \pmod 4 and \left(\frac{a}{b}\right) = \left(\frac{b}{a}\right) otherwise for a and b odd

Algorithm to compute is in O(\ell^2)

1.9.7 the group of quadratic residues (QR)

Let QR_n be the subgroup of Z_n^* of all quadratic residues.

• x \in QR_n \implies \left(\frac{x}{n}\right) = 1
• x, y \in QR_n \implies xy \in QR_n
• x \in QR_n, y \in Z_n^* \setminus QR_n \implies xy \in Z_n^* \setminus QR_n
• for p prime x, y \in Z_p^* \setminus QR_p \implies xy \in QR_p

1.10 factoring problem

1. Gen(1^\lambda) \to n
2. \mathcal A(n) \to (p, q)
3. return_{p\cdot q = n \land p, q \in \{2, \cdots, n-1\}}

1.10.1 RSA factoring / RSA square roots

1. RSA-Gen(1^\lambda) \to n
2. \mathcal A(n) \to (p, q)
3. return_{p\cdot q = n \land p, q \in \{2, \cdots, n-1\}}

\iff

1. RSA-Gen(1^\lambda) \to n
2. pick x \in QR_n
3. \mathcal A(n, x) \to y
4. return_{y^2 \bmod n = x}

1.10.2 lemma

y_0, y_1 \in Z_n

\begin{cases} y_0^2 &\equiv y_1^2 \pmod n \\ y_0 &\not\equiv y_1 \pmod n \\ y_0 &\not\equiv -y_1 \pmod n \\ \end{cases} \implies gcd(y_0 - y_1, n) \notin \{1, n\}

1.11 RSA problems

Note: \lambda(n) is the exponent of the group Z_n^*.

RSA-Full \lambda-factoring \implies RSA-Computing order in Z_n^* \implies RSA-Computing \lambda(n) \iff RSA-Factoring.

\begin{gather*} \text{RSADP} \impliedby &\text{RSAKRP}& \impliedby &\text{GOP}& \\ &\Downarrow& &\Updownarrow& \\ &\text{EMP}& \implies &\text{RSAFP}& \\ \end{gather*}

1. RSADP - decryption problem. Given n, e, y find x
2. RSAKRP - key recovery problem. Given n, e find d
3. GOP - group order problem. Given n find \varphi(n)
4. EMP - exponent multiple problem. Given n find a multiple of \lambda(n)
5. RSAFP - factorization problem. Given n find p and q