A category C is a directed graph (C_0, C_1) (objects and morphisms) equipped with composition maps
\gamma_{a,b,c} : C(a, b) \times C(b, c) \to C(a, c) : (f, g) \mapsto g \circ f
For \forall_{a, b, c} \in C_0 satisfying the following axioms:
A directed graph G consists of a pair of classes G_0 (vertices) and G_1 (edges) equipped with two maps \text{dom} : G_1 \to G_0 and \text{cod} : G_1 \to G_0.
So for a directed graph x \stackrel{f}{\longrightarrow} y, \text{dom}(f) = x and \text{cod}(f) = y
A subgraph G' of a directed graph G consists of a pair of subclasses G'_0 \subseteq G_0 and G'_1 \subseteq G_1 such that \text{dom}[G_1'] \cup \text{cod}[G'_1] \subseteq G_0'
When objects and morphisms are sets then the category is called small.
A subcategory C' of a category C consists of a subgraph (C_0', C_1') that is closed under composition of morphisms and such that \text{Id}_c \in C_1' for all c \in C_0'. It is full if C'(a, b) = C(a, b) for all a, b \in C_0' and is wide if C'_0 = \text{Ob}~C
Given two categories C and D, their product is a category C \times D and specified by
\text{Ob}(C \times D) = \text{Ob}~C \times \text{Ob}~D
and
\forall_{c, c' \in \text{Ob}~C}\forall_{d, d' \in \text{Ob}~D} (C \times D)((c, d), (c', d')) = C(c, c') \times D(d, d')
Then \text{Id}_{(c, d)} = (\text{Id}_c, \text{Id}_d)
Given a category C we define a category of morphisms C^\to where \text{Ob}~C^\to = \text{Mor}~C and where for every couple f : a \to b, g : c \to d of morphisms of C,
C^\to(f, g) = \{(h : a \to c, k : b \to d) \in \text{Mor}~C \times \text{Mor}~C | g \circ h = k \circ f : a \to d\}
For a category C its opposite category C^{op} is \text{Ob}~C^{op} = \text{Ob}~C and C^{op}(a, b) = C(b, a)
Given a morphism f : a \to b in C is an isomorphism, denoted \stackrel{\simeq}{\to} if it admits an inverse, ie there is a morphism g : b \to a such that g \circ f = \text{Id}_a and f \circ g = \text{Id}_b. a and b are called isomorphic.
A morphism between categories. A functor F: C \to D is a pair of maps F_{\text{Ob}} : \text{Ob}~C \to \text{Ob}~D and F_{\text{Mor}} : \text{Mor}~C \to \text{Mor}~D such that:
F_{\text{Mor}}(f) : F_{\text{Ob}}(a) \to F_{\text{Ob}}(b)
where
F_{\text{Mor}}(\text{Id}_c) = \text{Id}_{F_{\text{Ob}(c)}}
and
F_{\text{Mor}}(g \circ f) = F_{\text{Mor}}(g) \circ F_{\text{Mor}}(f)
Functors are composable in an associative manner
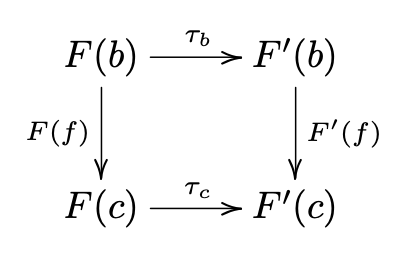
Let F, F' : C \to D be functors. A natural transformation \tau : F \to F' consists of a map
\tau : \text{Ob}~C \to \text{Mor}~D : c \mapsto \tau_c
such that for all c \in \text{Ob}~C
\tau_c \in D(F(c), F'(c))
and all morphisms f : b \to c in C, the diagram commutes

No more notes will appear. I dropped the course due to lack of prerequisite knowledge.